미래를 예측하고 대비하는 일은 비즈니스의 가장 핵심적인 부분입니다. 전력 수요를 예측해야 발전소를 증설할 수 있고, 콜센터의 통화수를 예측해야 적정한 수의 상담원을 배치할 수 있습니다. 예측 모델은 여러가지 변수를 포함할 수 있지만, 과거의 이력을 기반으로 미래의 추세를 예측한다는 점에서는 공통적입니다.
가장 간단한 단순회귀분석부터, 다중회귀분석, 딥러닝에 이르기까지 여러가지 모델링 방법이 있지만, 여기에서는 시계열 데이터에 쉽게 적용할 수 있으면서도 좋은 결과를 보여주는 ETS 모델을 알아보도록 하겠습니다.
ETS 모델은 업계에서 널리 사용되는 시계열 예측 모델로서, 지수평활법(Exponential Smoothing)을 기반으로 합니다. 지수평활법은 과거의 관측치에 시간의 흐름에 따른 가중치를 주고 합산하여 미래를 예측하는 방식입니다. 단순 지수평활법 (Single Exponential Smoothing) 에서 출발하여 하나씩 살펴보면 ETS 모델을 이해할 수 있습니다.
지수평활법: Exponential Smoothing
단순 지수평활법 (Single Exponential Smoothing)은 다음 예측치 (St)를 현재 값 (yt−1)과 이전 예측치(St−1)의 합산으로 계산합니다. 알파(α)는 0보다 크고 1보다 작은 스무딩 매개변수입니다:
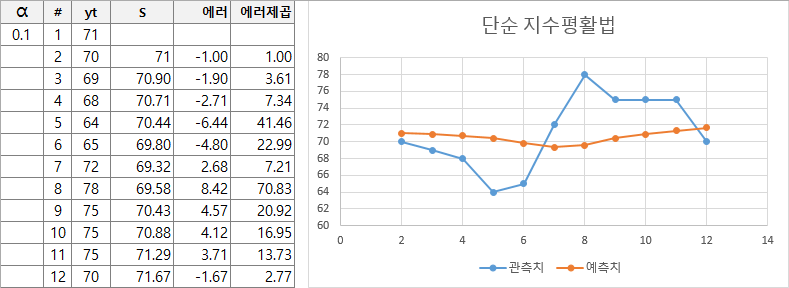
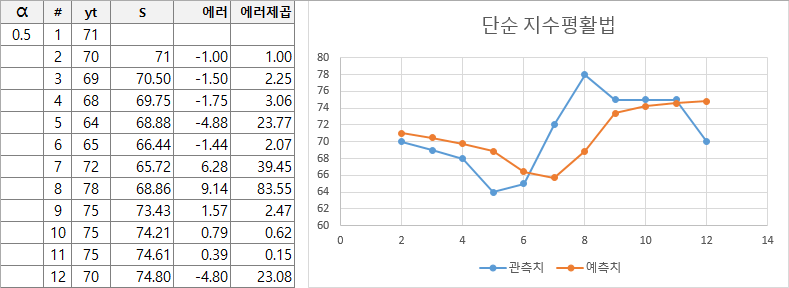
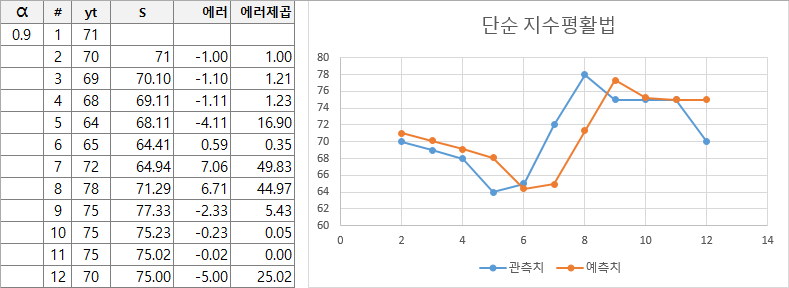
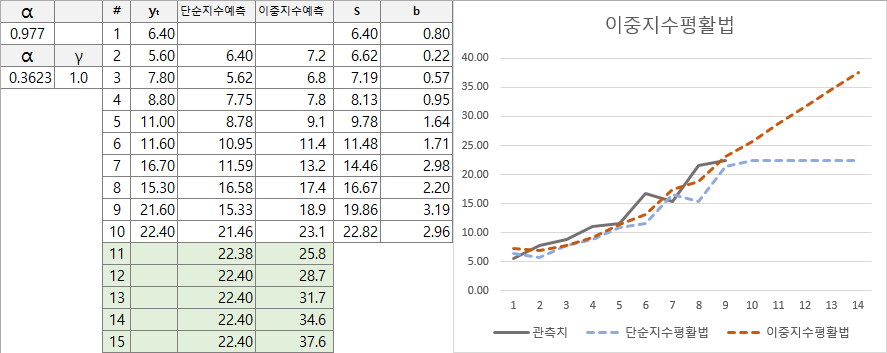
St = α yt−1 + (1−α) St−1실제 이 수식이 어떻게 동작하는지 예제 값을 넣어서 직관적으로 이해해볼 수 있습니다. 아래의 예제는 엑셀로 수식을 만들어서 스무딩 매개변수의 조정에 따른 변화를 표현한 것입니다.
매우 단순한 수식이지만 스무딩 매개변수에 따라 원본 그래프에 근접하게 변화하는 모습을 볼 수 있습니다. 최적의 스무딩 매개변수를 찾으면 해당 수식을 이용하여 미래의 값도 재귀적으로 예측할 수 있습니다.
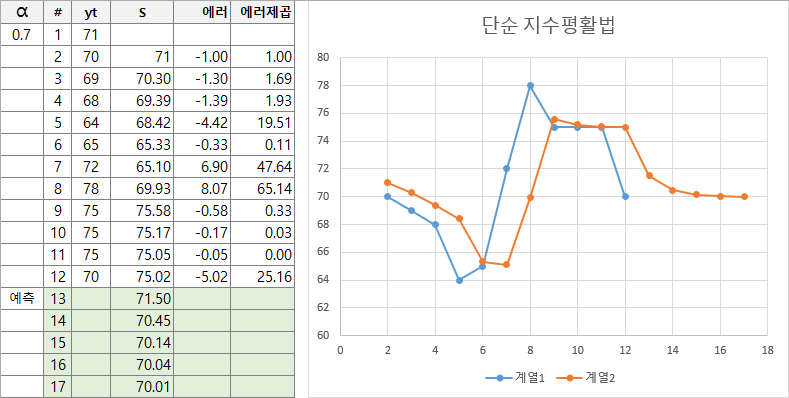
13번 행부터는 관측치가 없기 때문에 y를 마지막 값으로 고정하고 계산하면 위와 같이 예측치가 계산됩니다. 즉, 시계열 예측이 스무딩 매개변수에 따른 모형의 에러를 최소화하는 최적화 문제로 변환된 것입니다.
그러나, 단순 지수평활법의 단점은 추세가 있는 경우 잘 모델링하지 못한다는 점입니다. 이중 지수평활법 (Double Exponential Smoothing) 은 이러한 단점을 보완합니다. 아래의 예제는 이미 각 모델에 대해 최적으로 선정된 스무딩 매개변수 값을 사용하여 계산된 결과를 보여줍니다.
이중 지수평활법은 두 개의 방정식을 사용합니다.
St = α yt + (1 − α) (St−1 + bt−1)
bt = γ (St - St-1) + (1 − γ) bt−1
Ft+m = St + mbt
첫번째 수식은 이전 St-1 값에 추세변화량을 더하여 기저를 생성합니다. 두번째 수식은 추세변화량을 보정하는 역할을 수행합니다. 예측치는 기저와 추세변화량을 합산한 값입니다. 위의 그래프를 통해 단순 지수평활법과 이중 지수평활법의 예측 특성 차이를 확인할 수 있습니다.
이렇게 이중 지수평활법은 추세를 반영하지만 여기에 더해서 계절성 (Seasonality)이 있는 경우를 잘 반영하지 못합니다. 이 때문에 삼중 지수평활법 (Triple Exponential Smoothing) 혹은 홀트-윈터스 모델 (Holt-Winters) 이라 불리는 방법이 제안되게 됩니다.
ETS 모델
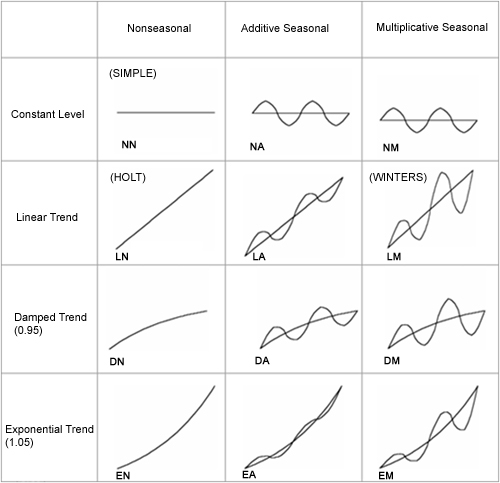
ETS 모델은 Error, Trend, Seasonality 3가지 요소로 구성된 모델을 의미합니다. 시계열 데이터는 추세의 특성과, 계절성을 각각 조합하여 다음과 같이 12가지의 유형을 상정할 수 있습니다.
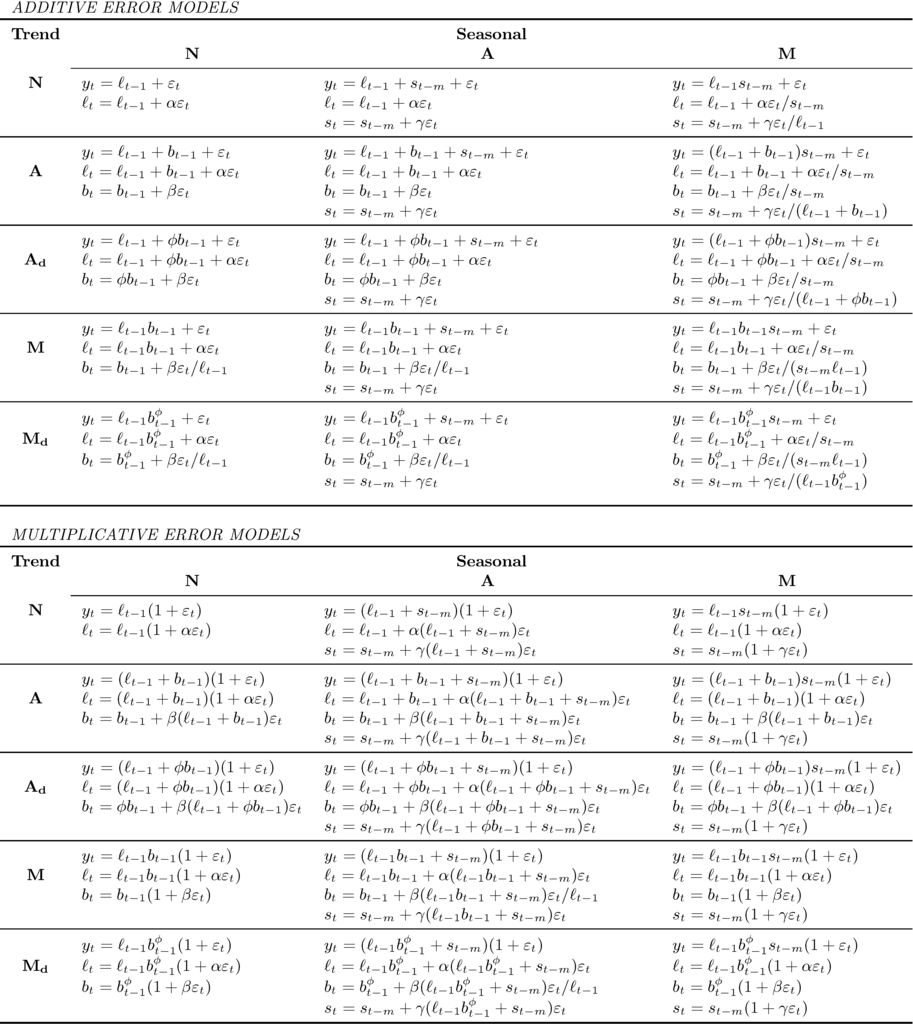
각 모델을 수식으로 표현하면 아래와 같습니다. 예를 들어, 에러, 추세, 계절성이 모두 가산적인 모델이라면 ETS(A,A,A) 혹은 ETS AAA 모델로 표기합니다. 계절성이 없는 가산적 모델이라면 ETS(A,A,N)에 해당됩니다.
- N: 상수 모델 (Constant)
- A: 가산적 모델 (Additive)
- Ad: 감쇄하는 가산적 모델 (Damped Additive)
- M: 승법적 모델 (Multiplicative)
- Md: 감쇄하는 승법적 모델 (Damped Multiplicative)
forecast 커맨드
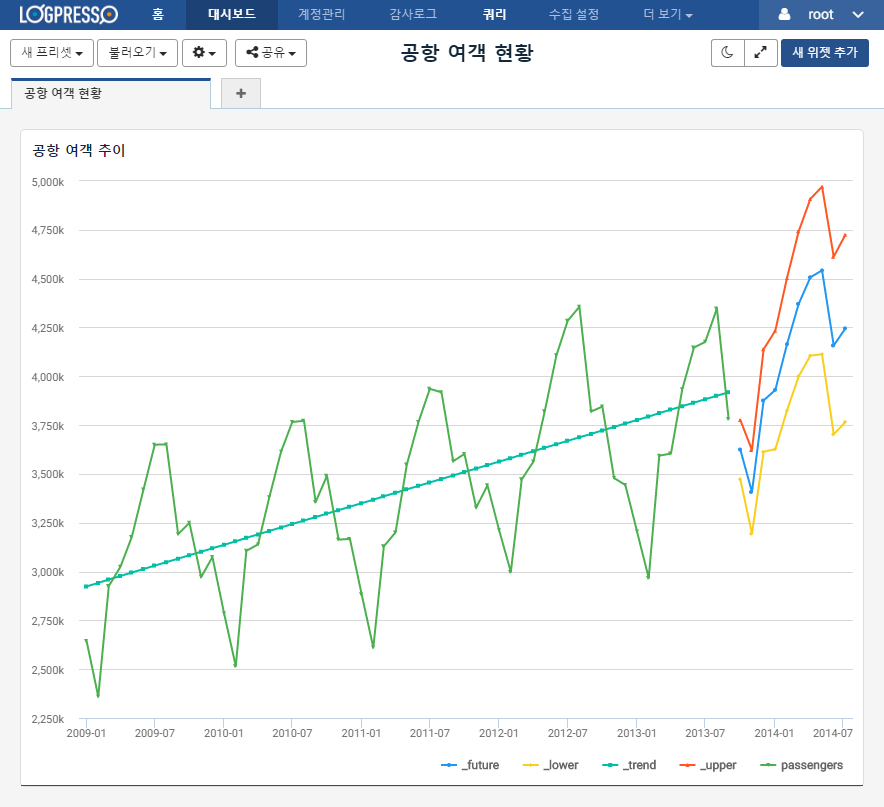
로그프레소는 주어진 시계열 데이터에 대해 위와 같이 다양한 ETS 모델을 대상으로 에러를 최소화하는 시계열 모형을 자동으로 탐색합니다. 예측된 값은 _future 필드로 출력되며, 추세 (_trend), 상위 95% 신뢰구간 (_upper), 하위 95% 신뢰구간 (_lower) 필드를 동시에 출력합니다.